2020-수학-가형-홀수-26¶
문제¶

풀이¶
from scipy.optimize import minimize
from pylab import figure, cm
import numpy as np
import matplotlib.pyplot as plt
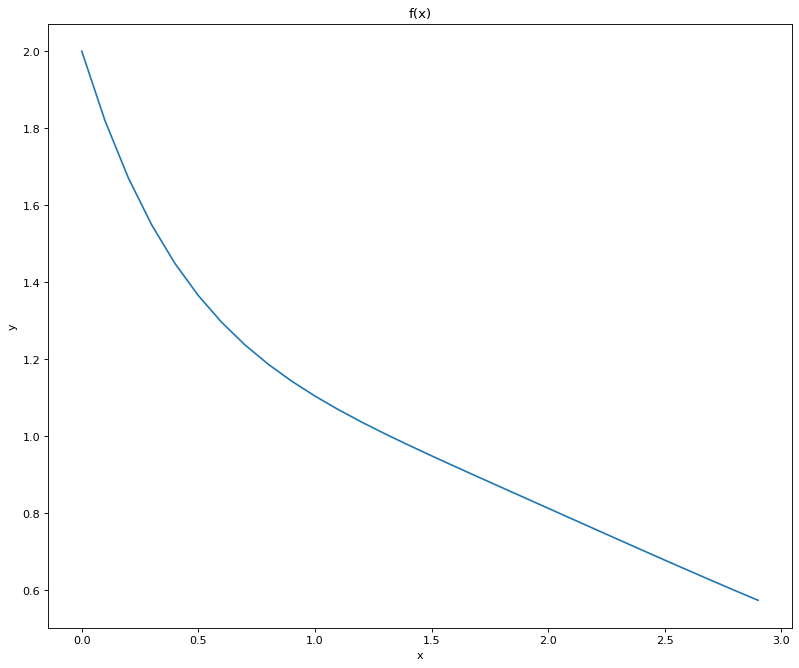
def f(x):
return (x**2+2)*np.exp(-x)
x = np.arange(0.0, 3.0, 0.1)
y = f(x)
fig = figure(num=None, figsize=(12, 10), dpi=80, facecolor='w', edgecolor='k')
plt.plot(x,y)
plt.title('f(x)')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
x = np.arange(np.min(y),np.max(y),0.1)
y = np.zeros(x.shape)
def diff(x,a):
yt = f(x)
return (yt - a )**2
for idx,x_value in enumerate(x):
res = minimize(diff, 1.0, args=(x_value), method='Nelder-Mead', tol=1e-6)
y[idx] = res.x[0]
fig = figure(num=None, figsize=(12, 10), dpi=80, facecolor='w', edgecolor='k')
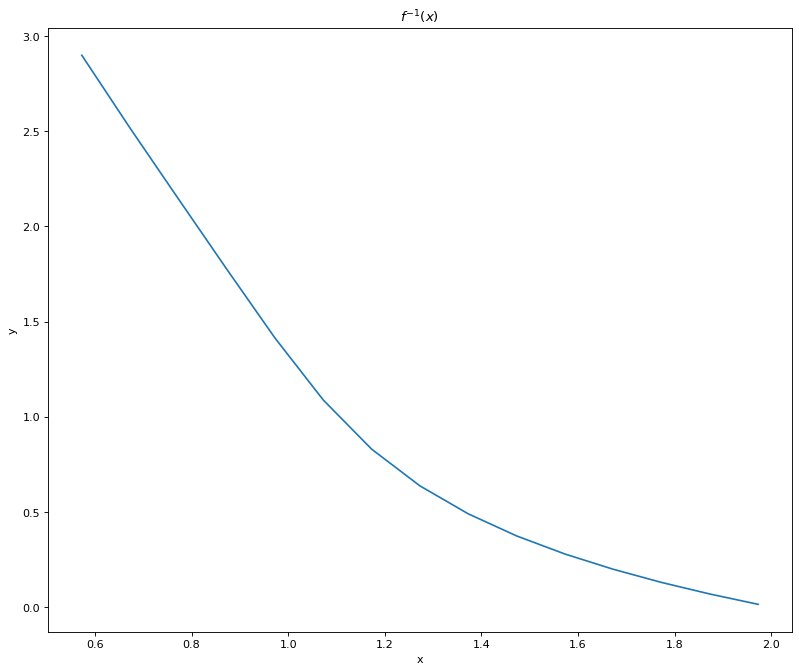
plt.plot(x,y)
plt.title(r'$f^{-1}(x)$')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
def f_inverse(x_value):
res = minimize(diff, 1.0, args=(x_value), method='Nelder-Mead', tol=1e-20)
return res.x[0]
def g(x):
return f_inverse(10*x-8)
f_inverse(2)
7.888609052210118e-31
g(1)
7.888609052210118e-31
deltas = [10**(-n) for n in range(0,10)]
for h in deltas:
print(abs(g(1+h)-0)/h)
1.229097035114094
3.470024817843762
4.7655294815361975
4.975165451984693
4.997501665441108
4.999750016647656
4.999975000075101
4.999997505805714
4.999999720922693
5.0000004137018585
