2019-수학-가형-홀수-14¶
문제¶
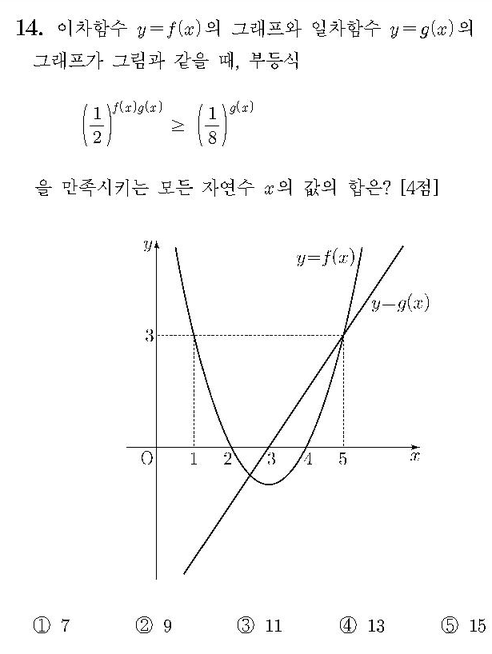
풀이¶
from sympy import *
def calc_parabola_vertex(x1, y1, x2, y2, x3, y3):
'''
Adapted and modifed to get the unknowns for defining a parabola:
http://stackoverflow.com/questions/717762/how-to-calculate-the-vertex-of-a-parabola-given-three-points
'''
denom = (x1-x2) * (x1-x3) * (x2-x3);
A = (x3 * (y2-y1) + x2 * (y1-y3) + x1 * (y3-y2)) / denom;
B = (x3*x3 * (y1-y2) + x2*x2 * (y3-y1) + x1*x1 * (y2-y3)) / denom;
C = (x2 * x3 * (x2-x3) * y1+x3 * x1 * (x3-x1) * y2+x1 * x2 * (x1-x2) * y3) / denom;
return A,B,C
calc_parabola_vertex(1,3,2,0,4,0)
(1.0, -6.0, 8.0)
l = Line(Point(3,0),Point(5,3))
l.equation()
\[\displaystyle - 3 x + 2 y + 9\]
x, y = symbols('x y')
solve(-3*x+2*y+9,y)
[3*x/2 - 9/2]
f = x**2-6*x+8
g = Rational(3,2)*x-Rational(9,2)
p1 = plot(f, (x, 0, 6), show=False)
p2 = plot(g, (x, 0, 6), show=False)
p1.append(p2[0])
p1.show()
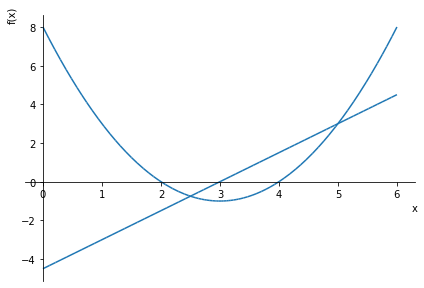
sum=0
for n in range(100):
if (f*g-3*g).subs(x,n)<=0:
print(n)
sum+=n
sum
0
1
3
4
5
13
