2019-수학-가형-홀수-19¶
문제¶
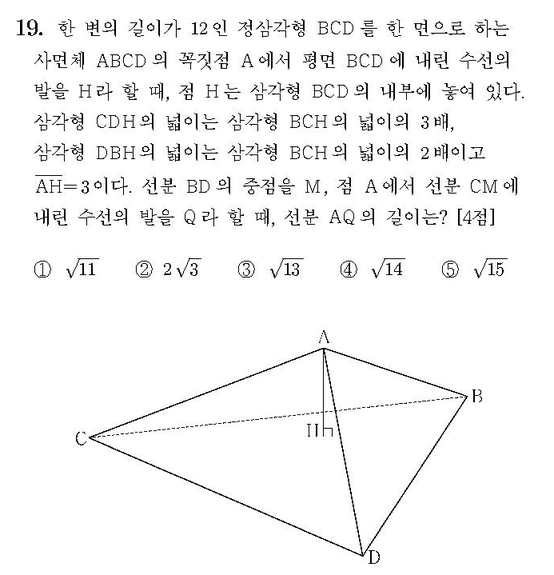
풀이¶
from sympy import *
r, x, y, z, k = symbols('r x y z k', real=True)
B = Point(r*cos(0),r*sin(0))
C = Point(r*cos(2*pi/3),r*sin(2*pi/3))
D = Point(r*cos(4*pi/3),r*sin(4*pi/3))
eqn = B.distance(C)-12
r_sol = solve(eqn,r)
r_sol
[-4*sqrt(3), 4*sqrt(3)]
B,C,D = [_.subs(r,r_sol[1]) for _ in [B,C,D]];
B,C,D
(Point2D(4*sqrt(3), 0), Point2D(-2*sqrt(3), 6), Point2D(-2*sqrt(3), -6))
H = Point(x,y)
eqns = [Line(B,C).distance(H)-k, Line(C,D).distance(H)-3*k, Line(B,D).distance(H)-2*k]
nsolve(eqns, [x,y,k], [0,0,0])
\[\begin{split}\displaystyle \left[\begin{matrix}1.73205080756888\\1.0\\1.73205080756888\end{matrix}\right]\end{split}\]
#x = sqrt(3)
#y = 1
#k = sqrt(3)
for _ in [Line(B,C).distance(H)-k, Line(C,D).distance(H)-3*k, Line(B,D).distance(H)-2*k]:
print(_.subs({x:sqrt(3),y:1,k:sqrt(3)}))
0
0
0
AH = 3
A=Point(x,y,AH).subs({x:sqrt(3),y:1,k:sqrt(3)})
B,C,D = [Point3D(_) for _ in [B,C,D]]
M = (B+D)/2
Line(C,M).distance(A)
\[\displaystyle \sqrt{13}\]
