2020-수학-가형-홀수-24¶
문제¶
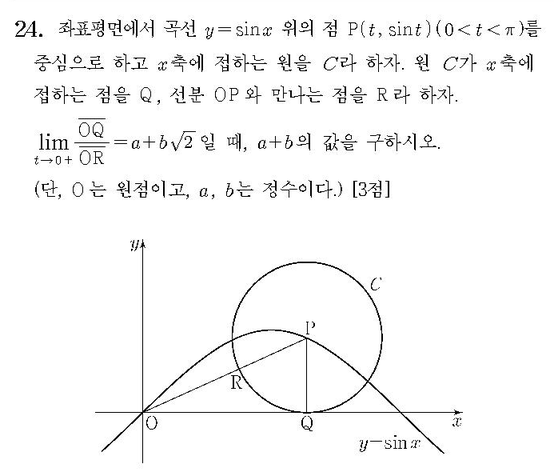
풀이¶
from sympy import *
t = symbols('t')
O = Point(0,0)
Q = Point(t, 0)
P = Point(t, sin(t))
c = Circle(P, sin(t))
l = Line(O, P)
R_candidates = intersection(c,l)
R_candidates
[Point2D(t*(sin(t) + sin(t)**2/sqrt(t**2 + sin(t)**2))/sin(t), sin(t) + sin(t)**2/sqrt(t**2 + sin(t)**2)),
Point2D(t*(sin(t) - sin(t)**2/sqrt(t**2 + sin(t)**2))/sin(t), sin(t) - sin(t)**2/sqrt(t**2 + sin(t)**2))]
R = Point(R_candidates[1])
R = simplify(R)
R
\[\displaystyle Point2D\left(\frac{t \left(\sin{\left(t \right)} - \frac{\sin^{2}{\left(t \right)}}{\sqrt{t^{2} + \sin^{2}{\left(t \right)}}}\right)}{\sin{\left(t \right)}}, \sin{\left(t \right)} - \frac{\sin^{2}{\left(t \right)}}{\sqrt{t^{2} + \sin^{2}{\left(t \right)}}}\right)\]
expr = (O.distance(Q))/(O.distance(R))
expr
\[\displaystyle \frac{\sqrt{t^{2}}}{\sqrt{\frac{t^{2} \left(\sin{\left(t \right)} - \frac{\sin^{2}{\left(t \right)}}{\sqrt{t^{2} + \sin^{2}{\left(t \right)}}}\right)^{2}}{\sin^{2}{\left(t \right)}} + \left(- \sin{\left(t \right)} + \frac{\sin^{2}{\left(t \right)}}{\sqrt{t^{2} + \sin^{2}{\left(t \right)}}}\right)^{2}}}\]
lim = limit(expr,t,0)
lim
\[\displaystyle \frac{1}{\sqrt{3 - 2 \sqrt{2}}}\]
simplify(lim)
\[\displaystyle \frac{1}{\sqrt{3 - 2 \sqrt{2}}}\]
min_diff = 1000.0
size = 10
for a in range(-size,size):
for b in range(-size,size):
val = a*sqrt(2)+b
diff = abs(lim-val).evalf()
if (diff-min_diff).evalf()<0:
min_diff = diff
ans = val
print([val, min_diff])
ans
[-10*sqrt(2) - 10, 26.5563491861040]
[-10*sqrt(2) - 9, 25.5563491861040]
[-10*sqrt(2) - 8, 24.5563491861040]
[-10*sqrt(2) - 7, 23.5563491861040]
[-10*sqrt(2) - 6, 22.5563491861040]
[-10*sqrt(2) - 5, 21.5563491861040]
[-10*sqrt(2) - 4, 20.5563491861040]
[-10*sqrt(2) - 3, 19.5563491861040]
[-10*sqrt(2) - 2, 18.5563491861040]
[-10*sqrt(2) - 1, 17.5563491861040]
[-10*sqrt(2), 16.5563491861040]
[1 - 10*sqrt(2), 15.5563491861040]
[2 - 10*sqrt(2), 14.5563491861040]
[3 - 10*sqrt(2), 13.5563491861040]
[4 - 10*sqrt(2), 12.5563491861040]
[5 - 10*sqrt(2), 11.5563491861040]
[6 - 10*sqrt(2), 10.5563491861040]
[7 - 10*sqrt(2), 9.55634918610405]
[8 - 10*sqrt(2), 8.55634918610405]
[9 - 10*sqrt(2), 7.55634918610405]
[8 - 9*sqrt(2), 7.14213562373095]
[9 - 9*sqrt(2), 6.14213562373095]
[8 - 8*sqrt(2), 5.72792206135786]
[9 - 8*sqrt(2), 4.72792206135786]
[8 - 7*sqrt(2), 4.31370849898476]
[9 - 7*sqrt(2), 3.31370849898476]
[8 - 6*sqrt(2), 2.89949493661167]
[9 - 6*sqrt(2), 1.89949493661167]
[8 - 5*sqrt(2), 1.48528137423857]
[9 - 5*sqrt(2), 0.485281374238570]
[8 - 4*sqrt(2), 0.0710678118654752]
[1 + sqrt(2), 0.e-128]
\[\displaystyle 1 + \sqrt{2}\]
PSLQ¶
from mpmath import *
pslq([(lim**2).evalf(), lim.evalf(), 1], tol=0.01)
[1, -2, -1]
x = symbols('x')
solve(x**2-2*x-1,x)
[1 - sqrt(2), 1 + sqrt(2)]
