2020-수학-가형-홀수-13¶
문제¶
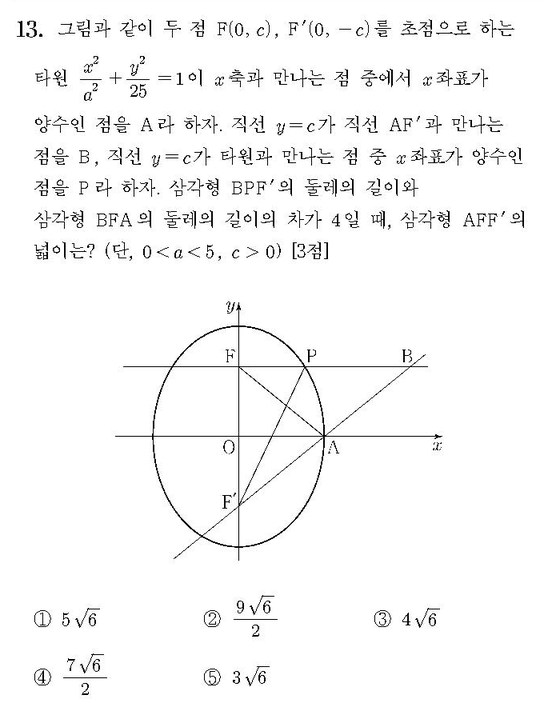
풀이¶
from sympy import *
a, c, t = symbols('a c t')
A = Point(a, 0);
F_plus = Point(0, c)
F_minus = Point(0,-c)
B = t*F_minus+(1-t)*A
B
\[\displaystyle Point2D\left(a \left(1 - t\right), - c t\right)\]
B = B.subs(t,-1)
B
\[\displaystyle Point2D\left(2 a, c\right)\]
x, y = symbols('x y')
ellipse = x**2/a**2+y**2/25-1
P_y = c
P_x = solve(ellipse.subs(y,P_y),x)
P_x
[-a*sqrt(25 - c**2)/5, a*sqrt(25 - c**2)/5]
P = Point(P_x[1], P_y)
length_BPF = B.distance(P)+P.distance(F_minus)+F_minus.distance(B)
length_BFA = B.distance(F_plus)+F_plus.distance(A)+A.distance(B)
eqn = length_BPF-length_BFA-4
eqn
\[\displaystyle - 2 \sqrt{a^{2} + c^{2}} + \sqrt{4 a^{2} + 4 c^{2}} + \sqrt{\frac{a^{2} \left(25 - c^{2}\right)}{25} + 4 c^{2}} - 2 \sqrt{a^{2}} + \sqrt{\left(- \frac{a \sqrt{25 - c^{2}}}{5} + 2 a\right)^{2}} - 4\]
eqn = simplify(eqn.subs(c**2, 25-a**2))
eqn
\[\displaystyle \frac{\sqrt{a^{2} \left(\sqrt{a^{2}} - 10\right)^{2}}}{5} + \frac{\sqrt{a^{4} - 100 a^{2} + 2500}}{5} - 2 \sqrt{a^{2}} - 4\]
val_a = solve(eqn,a)
val_a
[-sqrt(15), sqrt(15), 5 + 2*sqrt(15)]
val_a = sqrt(15)
val_c = sqrt(25-a**2).subs(a,val_a)
area = val_a*val_c
area
\[\displaystyle 5 \sqrt{6}\]
